1. 递归

1.1. 时空复杂度

时间复杂度：O(N) N：节点个数
空间复杂度：O(h) h：树的高度

1.2. 递归序

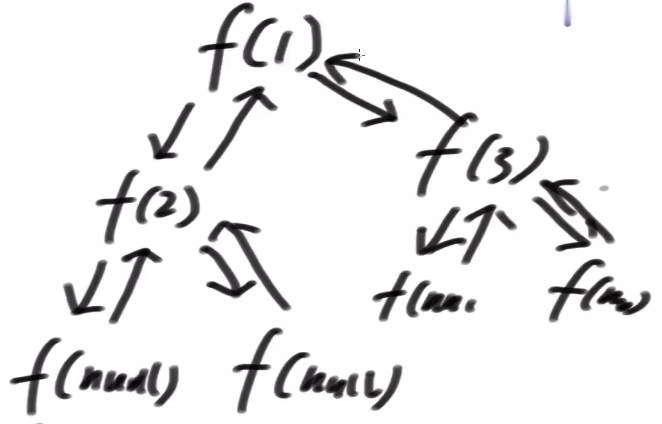
1-2-2-2-1-3-3-3-1

1.3. 前中后序

就是对递归序的加工

public static void process(Node root) {  
   if (root == null) {  
      return;  
   }  
   // 1 前序  
   System.out.print(root.value + " ");  
   process(root.left);  
   // 2 中序  
   //System.out.print(root.value + " ");
   process(root.right);  
   // 3 后序 
   //System.out.print(root.value + " "); 
}

1.4. 层序遍历

宽度优先遍历

public static void levelOrder(TreeNode root, int index, List result) {  
    if (root == null) return;  
  
    int length = result.size();  
    if (length <= index) {  
        for (int j = 0; j <= index - length; j++) {  
            result.add(length + j, null);  
        }  
    }  
  
    result.set(index, root.val);  
    levelOrder(root.left, 2*index, result);  
    levelOrder(root.right, 2*index + 1, result);  
}

2. 迭代

2.1. 时空复杂度

时间复杂度：O(N) N：节点个数
空间复杂度：O(h) h：树的高度

2.2. 先序遍历

public static void pre(Node head) {  
   System.out.print("pre-order: ");  
   if (head != null) {  
      Stack<Node> stack = new Stack<Node>();  
      stack.add(head);  
      while (!stack.isEmpty()) {  
         head = stack.pop();  
         System.out.print(head.value + " ");  
         if (head.right != null) {  
            stack.push(head.right);  
         }  
         if (head.left != null) {  
            stack.push(head.left);  
         }  
      }  
   }  
   System.out.println();  
}

2.3. 中序遍历

2.3.1. 算法逻辑

将整条左边界压入栈后开始弹出，并在弹出的每个节点的右孩子上尝试执行步骤1，即右孩子不为空就尝试将其左边界全部压入栈中

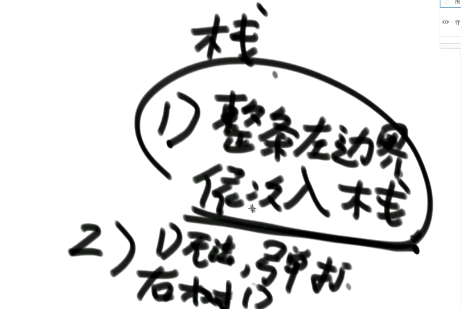
从左到右，将【左头】逐渐压入栈中，最终出栈的顺序就为【左头右】

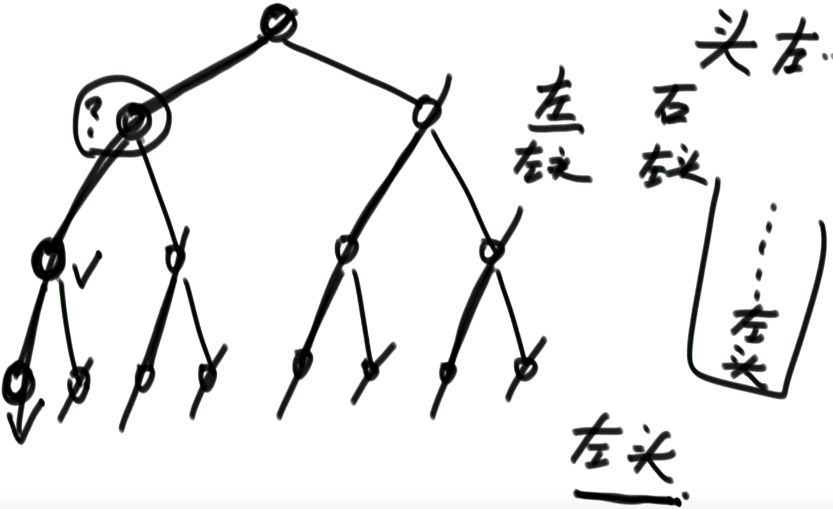
2.3.2. 代码实现

public static void in(Node cur) {  
   System.out.print("in-order: ");  
   if (cur != null) {  
      Stack<Node> stack = new Stack<Node>();  
      while (!stack.isEmpty() || cur != null) {  
         if (cur != null) {  
            stack.push(cur);  
            cur = cur.left;  
         } else {  
            cur = stack.pop();  
            System.out.print(cur.value + " ");  
            cur = cur.right;  
         }  
      }  
   }  
   System.out.println();  
}

2.4. 后序遍历

2.4.1. 方法一

先序遍历改为头右左，然后再利用另外一个栈倒序输出

public static void pos1(Node head) {  
   System.out.print("pos-order: ");  
   if (head != null) {  
      Stack<Node> s1 = new Stack<Node>();  
      Stack<Node> s2 = new Stack<Node>();  
      s1.push(head);  
      while (!s1.isEmpty()) {  
         head = s1.pop(); // 头 右 左  
         s2.push(head);  
         if (head.left != null) {  
            s1.push(head.left);  
         }  
         if (head.right != null) {  
            s1.push(head.right);  
         }  
      }  
      // 左 右 头  
      while (!s2.isEmpty()) {  
         System.out.print(s2.pop().value + " ");  
      }  
   }  
   System.out.println();  
}

2.4.2. 方法二

todo

2.5. 层序遍历

public static void level(Node head) {  
   if (head == null) {  
      return;  
   }  
   Queue<Node> queue = new LinkedList<>();  
   queue.add(head);  
   while (!queue.isEmpty()) {  
      Node cur = queue.poll();  
      System.out.println(cur.value);  
      if (cur.left != null) {  
         queue.add(cur.left);  
      }  
      if (cur.right != null) {  
         queue.add(cur.right);  
      }  
   }  
}

3. Morris遍历

3.1. 学习视频

要想透彻理解还得看左神
46:52

3.2. 时空复杂度

时间复杂度：O(N) N：节点个数
空间复杂度：O(1)

3.3. 算法本质

https://www.bilibili.com/video/BV1Bg411F7oo/?spm_id_from=333.999.0.0&vd_source=c5b2d0d7bc377c0c35dbc251d95cf204
05:04

回到上面节点(包括但不限于父节点)的方法：使用栈结构，递归遍历方法是使用系统的方法调用栈；而迭代遍历方法则是需要我们自己维护一个栈。
所以不管是递归还是迭代，都是用了栈的数据结构来回到上面节点。从而导致算法的空间复杂度为O(N)。
Morris算法为了降低算法的空间复杂度为O(1)，摒弃栈结构，而是使用子节点的右指针，确切的说是人为改造最右孩子的右指针，指向上面节点cur，来回到上面节点

3.4. Morris序

在Morris算法中，cur依次遍历节点的顺序，称为Morris序
Morris的前中后序也是对Morris序的加工

public static void morris(Node head) {
	if (head == null) {
		return;
	}
	Node cur = head;
	Node mostRight = null;
	while (cur != null) {
		// 先默认头节点左孩子为最右孩子
		// 判断cur是否有左树
		mostRight = cur.left;
		// 第一层大逻辑，判断是否有左孩子,如果有走if分支，如果没有cur向右移动
		if (mostRight != null) {
			// 获取真实的最右孩子
			while (mostRight.right != null && mostRight.right != cur){
				mostRight = mostRight.right;
			}
			// 从while出来 mostRight就是cur左树上的最右孩子

			// 最右孩子的右指针有2种情况
			// 第一种情况，指向空，说明是第一次走到，要将右指针指向cur
			// cur往左移动，继续处理它的左孩子的最右孩子的右指针
			if (mostRight.right == null) {
				mostRight.right = cur;
				cur = cur.left; // 向左移动 遍历以左孩子为根的子树
				continue;
			} else {
				// 第二种情况，指向cur，说明是第二次走到，要将指针复原为指向空的状态，同时向右移动，也就是说左边的已经处理完，再处理右边的子树
				mostRight.right = null;
			}
		}
		cur = cur.right;
	}
}

3.5. Morris先序

public static void morrisPre(Node head){  
   if (head == null) {  
      return;  
   }  
   Node cur = head;  
   Node mostRight = null;  
  
   while (cur != null) {  
      // 打印morris序  
      // System.out.print(cur.value + " ");      mostRight = cur.left;  
      // 第一层大逻辑，判断是否有左孩子  
      if (mostRight != null) {  
         // 有左孩子，左孩子有右孩子，一直往右出溜，找到最右孩子  
         while (mostRight.right != null && mostRight.right != cur) {  
            mostRight = mostRight.right;  
         }  
         // 最右孩子的右指针为空，第一次走到最右孩子  
         // 将最右孩子的右指针人为设置为cur         // cur往左移动，继续处理左孩子的最右孩子的右指针         if (mostRight.right == null) {  
            // ①能来到自己2次的节点，第一次来到的时候打印  
            System.out.print(cur.value + " ");  
            mostRight.right = cur;  
            cur = cur.left;  
            continue;  
         } else {  
            // 最右孩子的右指针已经指向了cur，将指针复原  
            // cur往右出溜，也就是说左边的已经处理完，再处理右边的子树            mostRight.right = null;  
         }  
      } else {  
         // ②没有左孩子，就是说只会来到自己一次的节点，直接打印  
         System.out.print(cur.value + " ");  
      }  
      // 没有左孩子，往右走  
      cur = cur.right;  
   }  
}

3.6. Morris中序

public static void morrisIn(Node head){  
   if (head == null) {  
      return;  
   }  
   Node cur = head;  
   Node mostRight = null;  
  
   while (cur != null) {  
      // 打印morris序   
      // System.out.print(cur.value + " ");  
      mostRight = cur.left;  
      // 第一层大逻辑，判断是否有左孩子  
      if (mostRight != null) {  
         // 有左孩子，左孩子有右孩子，一直往右出溜，找到最右孩子  
         while (mostRight.right != null && mostRight.right != cur) {  
            mostRight = mostRight.right;  
         }  
         // 最右孩子的右指针为空，第一次走到最右孩子  
         // 将最右孩子的右指针人为设置为cur         // cur往左移动，继续处理左孩子的最右孩子的右指针         if (mostRight.right == null) {  
            mostRight.right = cur;  
            cur = cur.left;  
            continue;  
         } else {  
            // 最右孩子的右指针已经指向了cur，将指针复原  
            // cur往右出溜，也就是说左边的已经处理完，再处理右边的子树            mostRight.right = null;  
         }  
      }  
      // 没有左孩子的节点只会遍历一次，直接打印  
      // 有左孩子的节点会遍历2次，第二次的时候把右指针复原后会走到这里来，打印      System.out.print(cur.value + " ");  
      // 没有左孩子，往右走  
      cur = cur.right;  
   }  
}

3.7. Morris后序

3.7.1. 实现逻辑

从morris序中可以看出，我们在有左子树的节点(能第二次遍历到)，第二次出现时处理逻辑：
逆序打印该节点的右边界(右边界指某个节点的左孩子及这个左孩子的所有右孩子)，比如第二次遍历到2时，它的右边界是4；第二次遍历到1时，它的右边界逆序是5,2；第二次遍历到3时，它的右边界是6，即：4-5-2-6，然后再加上整棵树的右边界的逆序，即7-3-1
整个加起来就是 4-5-2-6-7-3-1

3.7.2. 实现代码

public static void morrisPos(Node head) {  
   if (head == null) {  
      return;  
   }  
   Node cur = head;  
   Node mostRight = null;  
   while (cur != null) {  
      mostRight = cur.left;  
      if (mostRight != null) {  
         while (mostRight.right != null && mostRight.right != cur) {  
            mostRight = mostRight.right;  
         }  
         if (mostRight.right == null) {  
            mostRight.right = cur;  
            cur = cur.left;  
            continue;  
         } else {  
            mostRight.right = null;  
            printEdge(cur.left);  
         }  
      }  
      cur = cur.right;  
   }  
   printEdge(head);  
   System.out.println();  
}

public static void printEdge(Node head) {  
   Node tail = reverseEdge(head);  
   Node cur = tail;  
   while (cur != null) {  
      System.out.print(cur.value + " ");  
      cur = cur.right;  
   }  
   reverseEdge(tail);  
}  
  
public static Node reverseEdge(Node from) {  
   Node pre = null;  
   Node next = null;  
   while (from != null) {  
      next = from.right;  
      from.right = pre;  
      pre = from;  
      from = next;  
   }  
   return pre;  
}