1. 算法分类

内部排序：整个排序过程不需要借助于外部存储器（如磁盘等），所有排序操作都在内存中完成。
外部排序：参与排序的数据非常多，数据量非常大，计算机无法把整个排序过程放在内存中完成，必须借助于外部存储器（如磁盘）。外部排序最常见的是多路归并排序。可以认为外部排序是由多次内部排序组成。

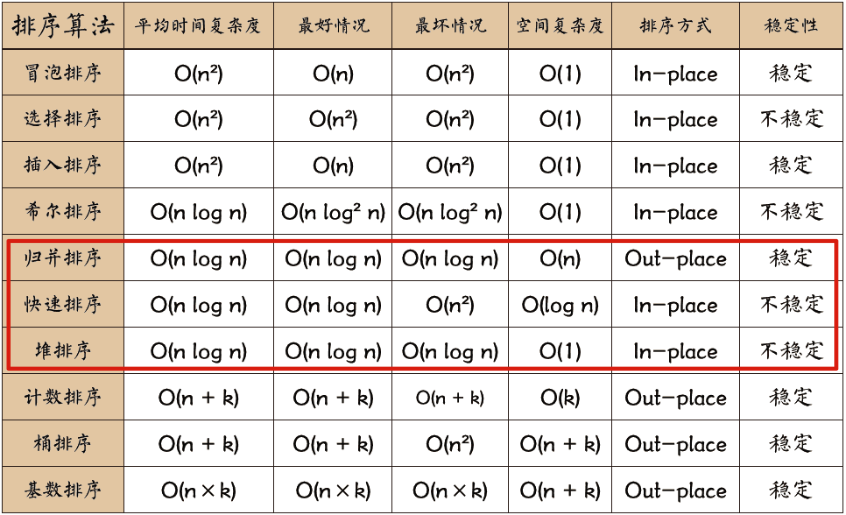
2. 算法比较

3. 冒泡排序(bubble sort)

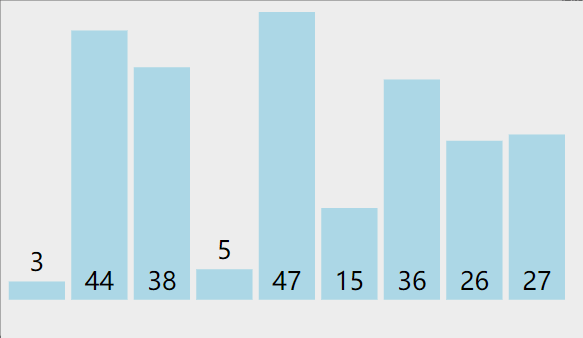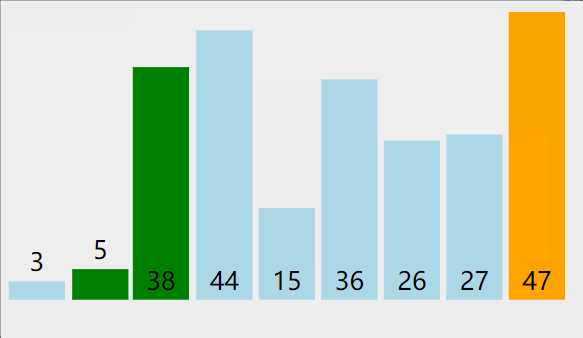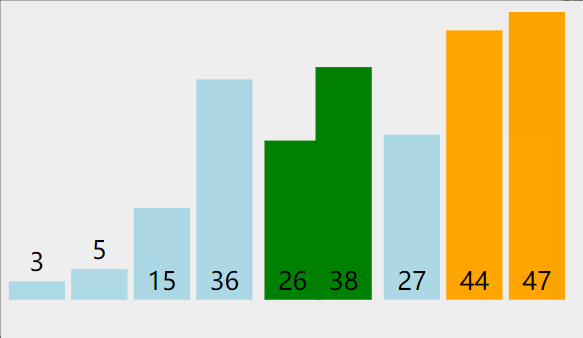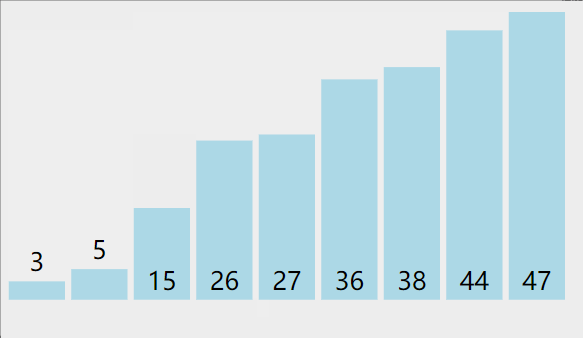
3.1. 算法思想

从左到右，两两比较，每轮确定一个数，共N-1轮，每一轮比较和交换次数都是N-1到1的递减数列

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

3.2. 代码实现

public static void bubbleSort(int[] arr) {  
    int temp = 0;  
    boolean flag = false;  
    for (int i = 0; i < arr.length - 1; i++) {  
        for (int j = 0; j < arr.length - i - 1; j++) {  
            if (arr[j] > arr[j + 1]) {  
                flag = true;  
                temp = arr[j];  
                arr[j] = arr[j + 1];  
                arr[j + 1] = temp;  
            }  
        }  
        System.out.println("第"+(i+1)+"趟排序后的数组");  
        System.out.println(Arrays.toString(arr));  
        if (!flag) {  
            break;  
        } else {  
            flag = false;  
        }  
    }  
}

3.3. 时间复杂度

冒泡排序使用了双层for循环，其中内层循环的循环体是真正完成排序的代码，所以，
我们分析冒泡排序的时间复杂度，主要分析一下内层循环体的执行次数即可。
在最坏情况下，也就是假如要排序的元素为{6,5,4,3,2,1}逆序，那么：
元素比较的次数为：
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
元素交换的次数为：
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
总执行次数为：
(N^2/2-N/2)+(N^2/2-N/2)=N^2-N;
按照大O推导法则，保留函数中的最高阶项那么最终冒泡排序的时间复杂度为O(N^2).

4. 选择排序(selection sort)

4.1. 算法思想

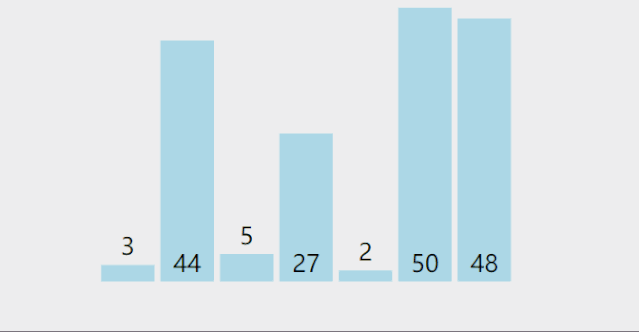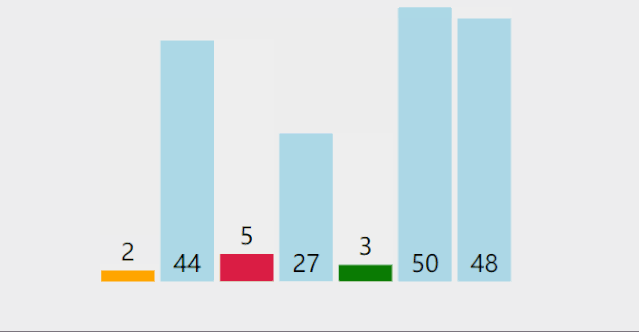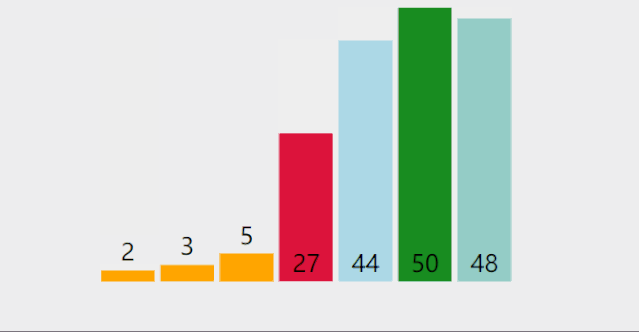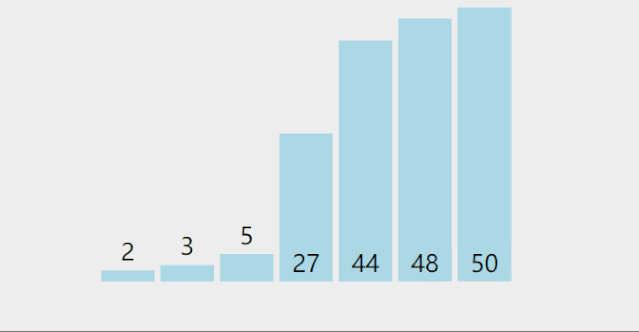
从左到右，拿第1个数分别与N-1个数比较(拿第2个数分别与N-2个数…)，共循环N-1次

在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾
以此类推，直到所有元素均排序完毕

4.2. 代码实现

//选择排序时间复杂度是 O(n^2)  
for (int i = 0; i < arr.length - 1; i++) {  
   int minIndex = i;  
   int min = arr[i];  
   for (int j = i + 1; j < arr.length; j++) {  
      if (min > arr[j]) { // 说明假定的最小值，并不是最小  
         min = arr[j]; // 重置min  
         minIndex = j; // 重置minIndex  
      }  
   }  
   // 将最小值，放在arr[0], 即交换  
   if (minIndex != i) {  
      arr[minIndex] = arr[i];  
      arr[i] = min;  
   }  
   //System.out.println("第"+(i+1)+"轮后~~");  
   //System.out.println(Arrays.toString(arr));// 1, 34, 119, 101
}

4.3. 时间复杂度

选择排序使用了双层for循环，其中外层循环完成了数据交换，内层循环完成了数据比较，所以我们分别统计数据
交换次数和数据比较次数：
数据比较次数：
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;

数据交换次数：N-1

时间复杂度：N^2/2-N/2+（N-1）=N^2/2+N/2-1;

根据大O推导法则，保留最高阶项，去除常数因子，时间复杂度为O(N^2);

因为选择排序过程中，交换次数比两两比较交换要少，所以时间上要比冒泡快一点

5. 插入排序(insertion sort)

5.1. 算法思想

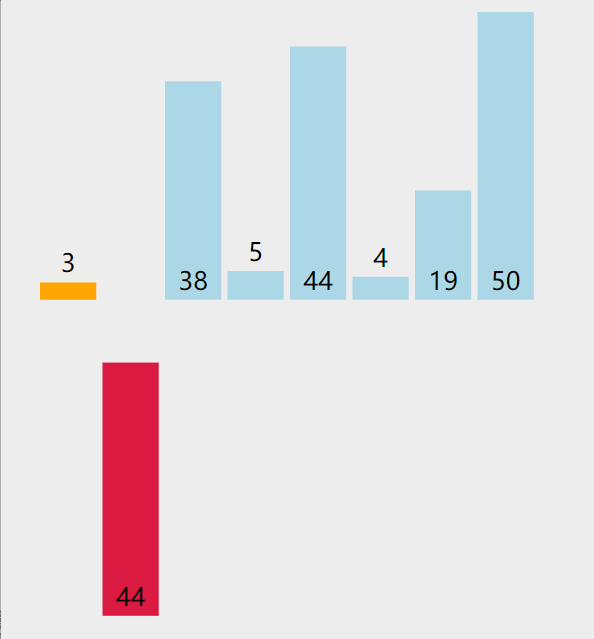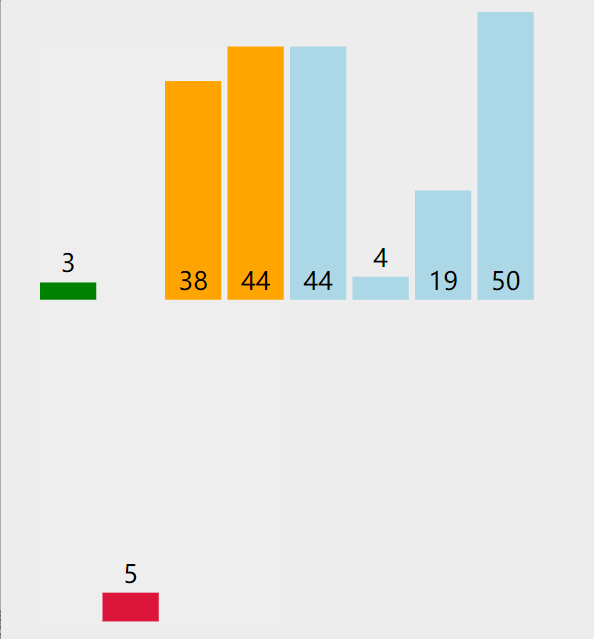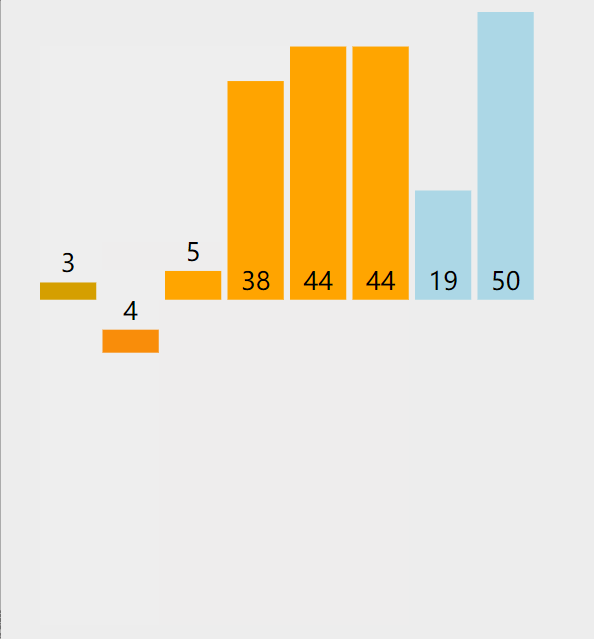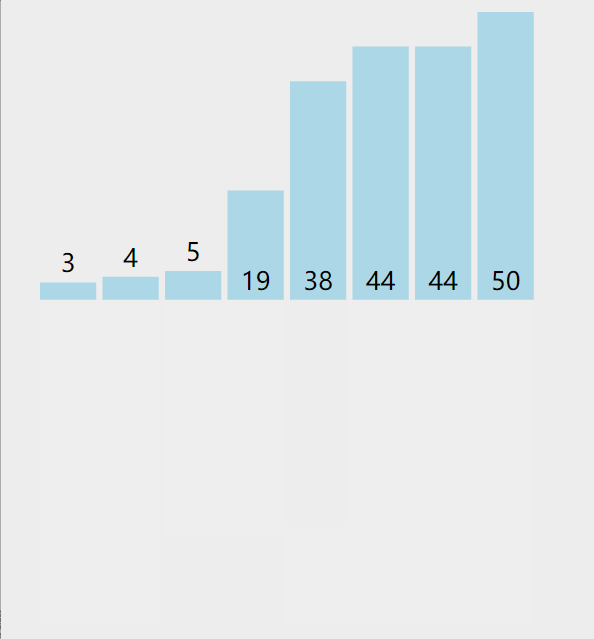
从第2个数开始，从右向左与前面i个数比较、交换

把所有的元素分为两组，已经排序的和未排序的；从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5

5.2. 代码实现

public static void sort(Comparable[] a){  
    for(int i=1;i<a.length;i++){  
        for(int j=i;j>0;j--){  
            //比较索引j处的值和索引j-1处的值，如果索引j-1处的值比索引j处的值大，则交换数据，如果不大，那么就找到合适的位置了，退出循环即可；  
            if (greater(a[j-1],a[j])){  
                exch(a,j-1,j);  
            }else{  
                break;  
            }  
        }  
    }  
}  
  
/*  
    比较v元素是否大于w元素 */private static  boolean greater(Comparable v,Comparable w){  
    return v.compareTo(w)>0;  
}  
  
/*  
数组元素i和j交换位置  
 */private static void exch(Comparable[] a,int i,int j){  
    Comparable temp;  
    temp = a[i];  
    a[i]=a[j];  
    a[j]=temp;  
}

5.3. 时间复杂度

插入排序使用了双层for循环，其中内层循环的循环体是真正完成排序的代码，所以，我们分析插入排序的时间复
杂度，主要分析一下内层循环体的执行次数即可。
最坏情况，也就是待排序的数组元素为{12,10,6,5,4,3,2,1}，那么：
比较的次数为：
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
交换的次数为：
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
总执行次数为：
(N^2/2-N/2)+(N^2/2-N/2)=N^2-N;
按照大O推导法则，保留函数中的最高阶项那么最终插入排序的时间复杂度为O(N^2).

6. 希尔排序(shell sort)

6.1. 算法思想

1.选定一个增长量gap，按照增长量gap作为数据分组的依据，对数据进行分组；
2.对分好组的每一组数据完成插入排序；
3.减小增长量，最小减为1，重复第二步操作。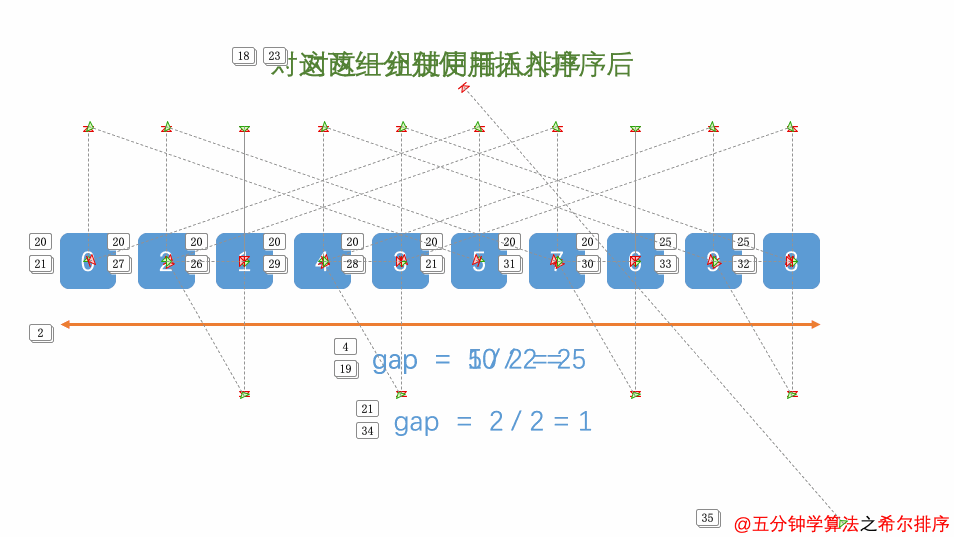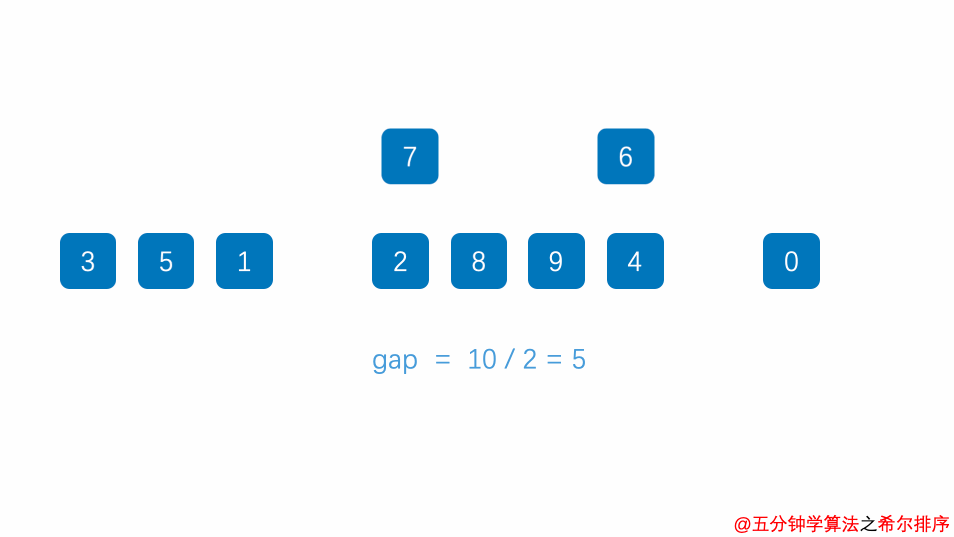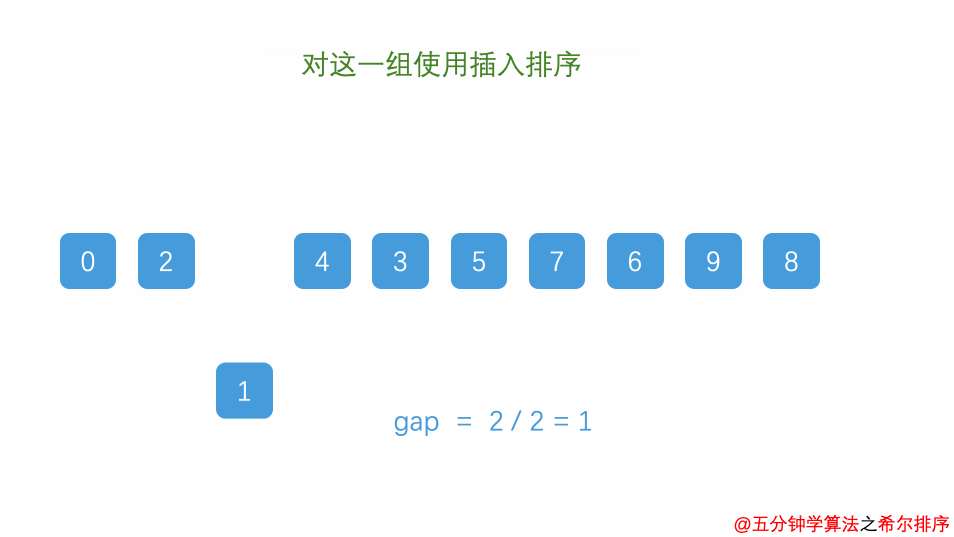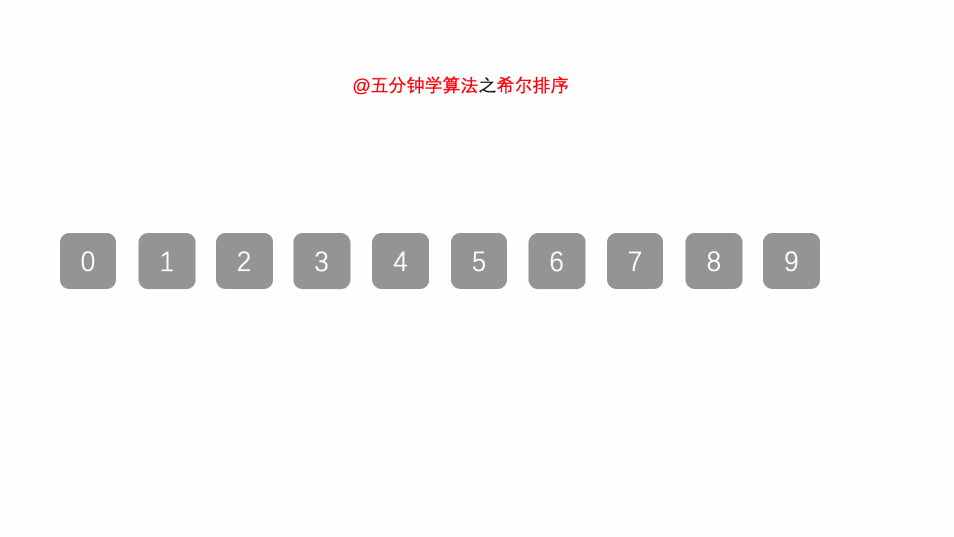

增长量gap的确定：增长量h的值每一固定的规则，我们这里采用以下规则：

int gap=1

while(gap<5){

  gap=2gap+1；//3,7

}

//循环结束后我们就可以确定h的最大值；

h的减小规则为：

gap=gap/2

6.2. 代码实现

public static void sort(Comparable[] a){
	//1.根据数组a的长度，确定增长量h的初始值；
	int h = 1;
	while(h<a.length/2){
		h=2*h+1;
	}
	//2.希尔排序
	while(h>=1){
		//排序
		//2.1.找到待插入的元素
		for (int i=h;i<a.length;i++){
			//2.2把待插入的元素插入到有序数列中
			for (int j=i;j>=h;j-=h){

				//待插入的元素是a[j],比较a[j]和a[j-h]
				if (greater(a[j-h],a[j])){
					//交换元素
					exch(a,j-h,j);
				}else{
					//待插入元素已经找到了合适的位置，结束循环；
					break;
				}
			}

		}
		//减小h的值
		h= h/2;
	}
}

6.3. 时间复杂度

todo

7. 归并排序(merge sort)

7.1. 算法思想

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

尽可能的一组数据拆分成两个元素相等的子组，并对每一个子组继续拆分，直到拆分后的每个子组的元素个数是1为止。
将相邻的两个子组进行合并成一个有序的大组；
不断的重复步骤2，直到最终只有一个组为止。

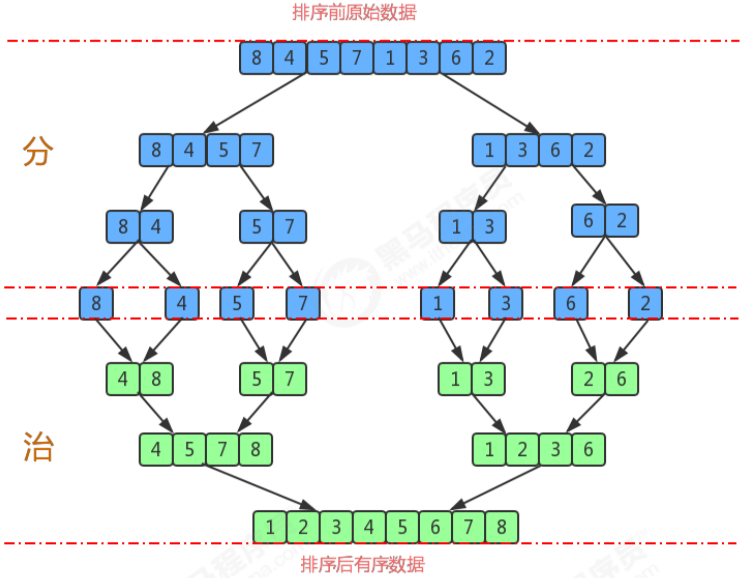
7.2. 代码实现

public static void mergeSort(int[] arr) {
	if (arr == null || arr.length < 2) {
		return;
	}
	mergeSort(arr, 0, arr.length - 1);
}

public static void mergeSort(int[] arr, int l, int r) {
	if (l == r) {
		return;
	}
	int mid = l + ((r - l) >> 1);
	mergeSort(arr, l, mid);
	mergeSort(arr, mid + 1, r);
	merge(arr, l, mid, r);
}

public static void merge(int[] arr, int l, int m, int r) {
	int[] help = new int[r - l + 1];
	int i = 0;
	int p1 = l;
	int p2 = m + 1;
	while (p1 <= m && p2 <= r) {
		help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
	}
	while (p1 <= m) {
		help[i++] = arr[p1++];
	}
	while (p2 <= r) {
		help[i++] = arr[p2++];
	}
	for (i = 0; i < help.length; i++) {
		arr[l + i] = help[i];
	}
}

public class Merge {
    //归并所需要的辅助数组
    private static Comparable[] assist;

    /*
       比较v元素是否小于w元素
    */
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w)<0;
    }

    /*
    数组元素i和j交换位置
     */
    private static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }


    /*
           对数组a中的元素进行排序
        */
    public static void sort(Comparable[] a) {
        //1.初始化辅助数组assist；
        assist = new Comparable[a.length];
        //2.定义一个lo变量，和hi变量，分别记录数组中最小的索引和最大的索引；
        int lo=0;
        int hi=a.length-1;
        //3.调用sort重载方法完成数组a中，从索引lo到索引hi的元素的排序
        sort(a,lo,hi);
    }

    /*
    对数组a中从lo到hi的元素进行排序
     */
    private static void sort(Comparable[] a, int lo, int hi) {
        //做安全性校验；
        if (hi<=lo){
            return;
        }

        //对lo到hi之间的数据进行分为两个组
        int mid = lo+(hi-lo)/2;//   5,9  mid=7

        //分别对每一组数据进行排序
        sort(a,lo,mid);
        sort(a,mid+1,hi);

        //再把两个组中的数据进行归并
        merge(a,lo,mid,hi);
    }

    /*
    对数组中，从lo到mid为一组，从mid+1到hi为一组，对这两组数据进行归并
     */
    private static void merge(Comparable[] a, int lo, int mid, int hi) {
        //定义三个指针
        int i=lo;
        int p1=lo;
        int p2=mid+1;

        //遍历，移动p1指针和p2指针，比较对应索引处的值，找出小的那个，放到辅助数组的对应索引处
        while(p1<=mid && p2<=hi){
            //比较对应索引处的值
            if (less(a[p1],a[p2])){
                assist[i++] = a[p1++];
            }else{
                assist[i++]=a[p2++];
            }
        }

        //遍历，如果p1的指针没有走完，那么顺序移动p1指针，把对应的元素放到辅助数组的对应索引处
        while(p1<=mid){
            assist[i++]=a[p1++];
        }
        //遍历，如果p2的指针没有走完，那么顺序移动p2指针，把对应的元素放到辅助数组的对应索引处
        while(p2<=hi){
            assist[i++]=a[p2++];
        }
        //把辅助数组中的元素拷贝到原数组中
        for(int index=lo;index<=hi;index++){
            a[index]=assist[index];
        }

    }

}

参考
https://www.bilibili.com/video/BV1XV4y1H7Yn?p=4&vd_source=c5b2d0d7bc377c0c35dbc251d95cf204
https://www.bilibili.com/video/BV1iJ411E7xW/?p=26&spm_id_from=pageDriver&vd_source=c5b2d0d7bc377c0c35dbc251d95cf204

7.3. 复杂度分析

时间复杂度：O(nlogn)

1
2
3

用树状图来描述归并，如果一个数组有8个元素，那么它将每次除以2找最小的子数组，共拆log8次，值为3，所以树共有3层,那么自顶向下第k层有2^k个子数组，每个数组的长度为2^(3-k)，归并最多需要2^(3-k)次比较。因此每层的比较次数为 2^k * 2^(3-k)=2^3,那么3层总共为 3*2^3。

假设元素的个数为n，那么使用归并排序拆分的次数为log2(n),所以共log2(n)层，那么使用log2(n)替换上面3*2^3中的3这个层数，最终得出的归并排序的时间复杂度为：log2(n)* 2^(log2(n))=log2(n)*n,根据大O推导法则，忽略底数，最终归并排序的时间复杂度为O(nlogn);

空间复杂度：O(N) ：归并排序需要一个与原数组相同长度的数组做辅助来排序
稳定性：归并排序是稳定的排序算法，temp[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];这行代码可以保证当左右两部分的值相等的时候，先复制左边的值，这样可以保证值相等的时候两个元素的相对位置不变。

8. 快速排序(quick sort)

8.1. 算法思想

快速排序是对冒泡排序的一种改进。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

算法步骤

1.找一个基准值，用两个指针分别指向数组的头部和尾部；

2.先从尾部向头部开始搜索一个比基准值小的元素，搜索到即停止，并记录指针的位置；

3.再从头部向尾部开始搜索一个比基准值大的元素，搜索到即停止，并记录指针的位置；

4.交换当前左边指针位置和右边指针位置的元素；

5.重复2,3,4步骤，直到左边指针的值大于右边指针的值停止。

8.2. 代码实现

public class Quick {
    /*
      比较v元素是否小于w元素
   */
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }



    /*
   数组元素i和j交换位置
    */
    private static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

    //对数组内的元素进行排序
    public static void sort(Comparable[] a) {
        int lo = 0;
        int hi = a.length-1;
        sort(a,lo,hi);
    }

    //对数组a中从索引lo到索引hi之间的元素进行排序
    private static void sort(Comparable[] a, int lo, int hi) {
        //安全性校验
        if (hi<=lo){
            return;
        }

        //需要对数组中lo索引到hi索引处的元素进行分组（左子组和右子组）；
        int partition = partition(a, lo, hi);//返回的是分组的分界值所在的索引，分界值位置变换后的索引

        //让左子组有序
        sort(a,lo,partition-1);

        //让右子组有序
        sort(a,partition+1,hi);
    }

    //对数组a中，从索引 lo到索引 hi之间的元素进行分组，并返回分组界限对应的索引
    public static int partition(Comparable[] a, int lo, int hi) {
       //确定分界值
        Comparable key = a[lo];
        //定义两个指针，分别指向待切分元素的最小索引处和最大索引处的下一个位置
        int left=lo;
        int right=hi+1;

        //切分
        while(true){
            //先从右往左扫描，移动right指针，找到一个比分界值小的元素，停止
            while(less(key,a[--right])){
                if (right==lo){
                    break;
                }
            }

            //再从左往右扫描，移动left指针，找到一个比分界值大的元素，停止
            while(less(a[++left],key)){
                if (left==hi){
                    break;
                }
            }
            //判断 left>=right,如果是，则证明元素扫描完毕，结束循环，如果不是，则交换元素即可
            if (left>=right){
                break;
            }else{
                exch(a,left,right);
            }
        }

        //交换分界值
        exch(a,lo,right);

       return right;
    }

}

8.3. 复杂度分析

快速排序的一次切分从两头开始交替搜索，直到left和right重合，因此，每一次切分的时间复杂度为O(n),但整个快速排序的时间复杂度和切分的次数相关。
最优情况：每一次切分选择的基准数字刚好将当前序列等分。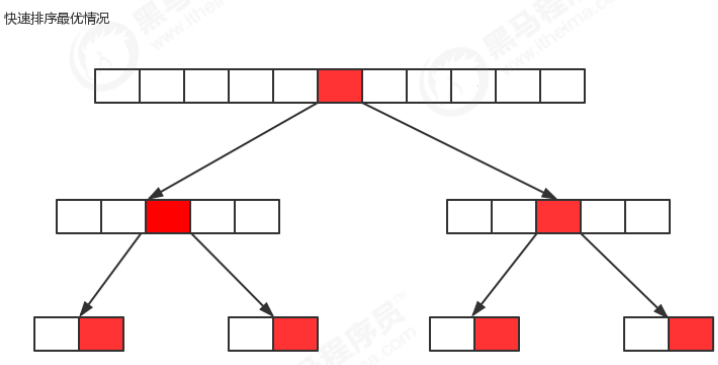

如果我们把数组的切分看做是一个树，那么上图就是它的最优情况的图示，共切分了logn次，所以，最优情况下快速排序的时间复杂度为O(nlogn);
最坏情况：每一次切分选择的基准数字是当前序列中最大数或者最小数，这使得每次切分都会有一个子组，那么总共就得切分n次，所以，最坏情况下，快速排序的时间复杂度为O(n^2);

空间复杂度与空间复杂度的分析情况类似，而空间用来记录划分点，最好情况是接近二分，所以是O(logn)。最坏情况是接近遍历所有，所以是O(n)，最终通过概率统计得出O(logn)。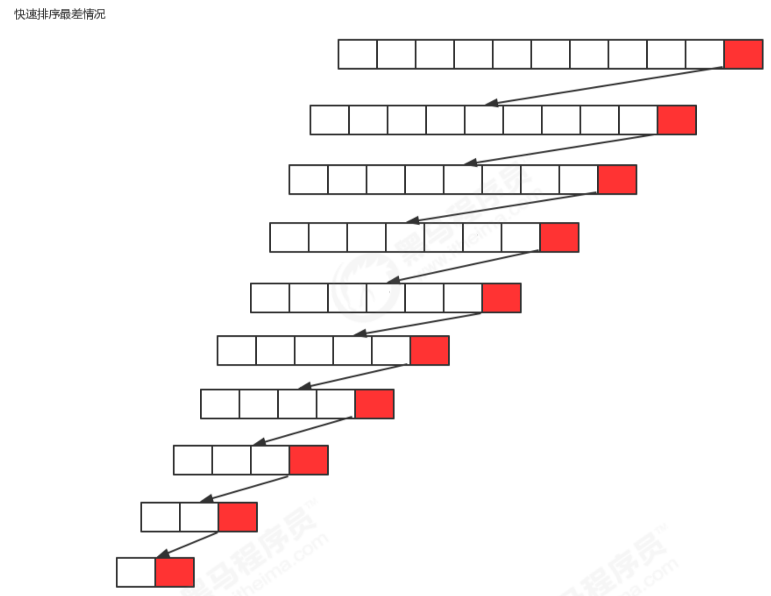

8.4. 快排VS归并

与归并排序类似，快速排序是另外一种分治的排序算法，它将一个数组分成两个子数组，将两部分独立的排序。快速排序和归并排序是互补的：归并排序将数组分成两个子数组分别排序，并将有序的子数组归并从而将整个数组排序，而快速排序的方式则是当两个数组都有序时，整个数组自然就有序了。在归并排序中，一个数组被等分为两半，归并调用发生在处理整个数组之前，也就是先mergeSort再merge。在快速排序中，切分数组的位置取决于数组的内容，递归调用发生在处理整个数组之后，也就是先分区后递归排序。

8.5. 参考

https://www.bilibili.com/video/BV1iJ411E7xW?p=35&vd_source=c5b2d0d7bc377c0c35dbc251d95cf204

https://www.bilibili.com/video/BV13g41157hK?p=4&vd_source=c5b2d0d7bc377c0c35dbc251d95cf204
02:06:39

9. 堆排序(heap sort)

堆排序是利用堆这种数据结构而设计的，是一种选择排序算法。它的最好、最坏、平均时间复杂度均为O(nlogn)。

堆的性质：完全二叉树

9.1. 大根堆

每个节点的值都大于或等于其左右孩子的值，以x为头的整棵树的最大值为x。左右孩子的大小关系无要求。
节点i的左孩子：2*i+1
节点i的右孩子：2*i+2
节点i的父节点：(i-1)/2

9.1.1. heapinsert

如何保持大根堆特性
每加入一个新节点，就与自己的父节点进行比较，如果大于父节点则交换，交换完之后再次与新父节点比较，依次循环，直到小于等于自己的父节点或者变成了根节点为止。

public static void heapInsert(int[] arr, int index) {
	while (arr[index] > arr[(index - 1) / 2]) {
		swap(arr, index, (index - 1) /2);
		index = (index - 1)/2 ;
	}
}

9.1.2. heapify

// 某个数在index，能否向下移动
public static void heapify(int[] arr, int index, int size) {
	int left = index * 2 + 1; //左孩子下标
	while (left < size) { //下方还有孩子
		//有右孩子 && 右孩子大于左孩子 --> 右孩子胜出，返回右孩子下标，否则返回左孩子下标。即左右两个孩子谁大返回谁的下标 
		int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
		//父亲和较大孩子之间谁的值大 返回谁的下标给largest
		largest = arr[largest] > arr[index] ? largest : index;

		//表示此时index位置的值就是最大值，不需要下移
		if (largest == index) {
			break;
		}

		//较大的孩子和父交换
		swap(arr, largest, index);
		//位置下移
		index = largest;
		//左孩子变化，然后进入下一次while循环
		left = index * 2 + 1;
	}
}

9.2. 算法思想

首先heapify，将数组变成堆
堆的首尾位置元素互换，就会将最大值放到堆的最后
堆size–，将最大值移除
再次heapify，周而复始

9.3. 代码实现

public static void heapSort(int[] arr) {
	if (arr == null || arr.length < 2) {
		return;
	}
	for (int i = 0; i < arr.length; i++) {
		heapInsert(arr, i);
	}
	int size = arr.length;
	swap(arr, 0, --size);
	while (size > 0) {
		heapify(arr, 0, size);
		swap(arr, 0, --size);
	}
}

public static void heapInsert(int[] arr, int index) {
	while (arr[index] > arr[(index - 1) / 2]) {
		swap(arr, index, (index - 1) /2);
		index = (index - 1)/2 ;
	}
}

public static void heapify(int[] arr, int index, int size) {
	int left = index * 2 + 1;
	while (left < size) {
		int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
		largest = arr[largest] > arr[index] ? largest : index;
		if (largest == index) {
			break;
		}
		swap(arr, largest, index);
		index = largest;
		left = index * 2 + 1;
	}
}

public static void swap(int[] arr, int i, int j) {
	int tmp = arr[i];
	arr[i] = arr[j];
	arr[j] = tmp;
}

9.4. 复杂度分析

时间复杂度：O(nlogn)
空间复杂度：O(1)

9.5. 稳定性

不稳定

9.6. 参考

https://www.bilibili.com/video/BV13g41157hK/?p=5&vd_source=c5b2d0d7bc377c0c35dbc251d95cf204
08:39

10. 桶排序(bucket sort)

10.1. 算法思想

设置一个定量的数组当作空桶子
寻访序列，并且把项目一个一个放到对应的桶子去。
对每个不是空的桶子进行排序。
从不是空的桶子里把项目再放回原来的序列中。

不同场景，设计不同的桶

按位数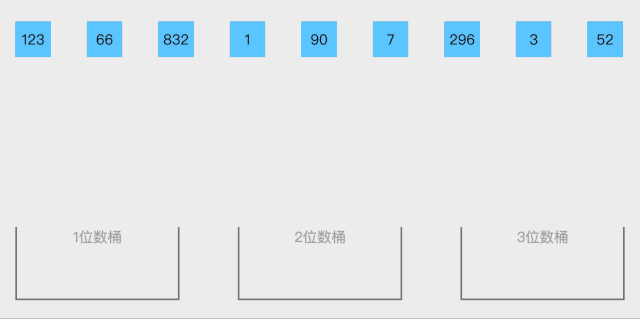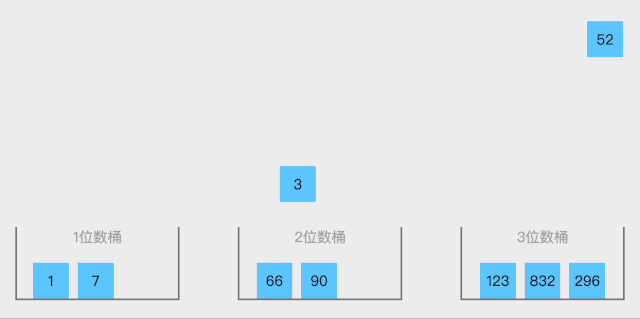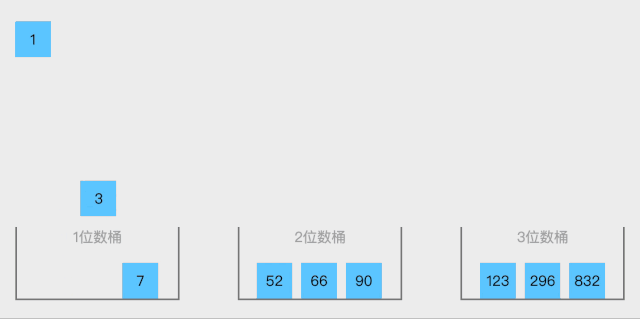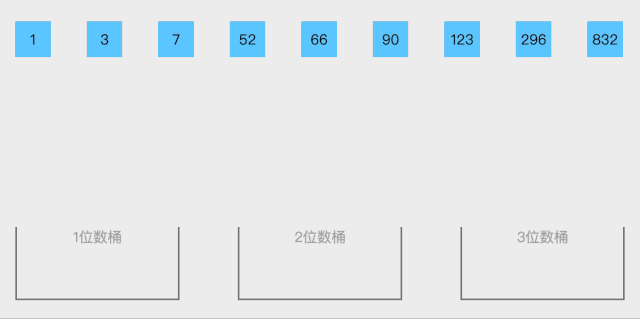

按范围

11. 基数排序(radix sort)

11.1. 算法思想

一种多关键字的排序算法，可用桶排序实现。

取得数组中的最大数，并取得位数；
arr为原始数组，从最低位开始取每个位组成radix数组；
对radix进行计数排序（利用计数排序适用于小范围数的特点）

12. 计数排序(count sort)

12.1. 算法思想

花O(n)的时间扫描一下整个序列 A，获取最小值 min 和最大值 max
开辟一块新的空间创建新的数组 B，长度为 ( max - min + 1)
数组 B 中 index 的元素记录的值是 A 中某元素出现的次数
最后输出目标整数序列，具体的逻辑是遍历数组 B，输出相应元素以及对应的个数

13. 总结

Java 提供的默认排序算法

Java提供的默认排序算法，具体是什么排序方式以及设计思路？这个问题本身就是有点陷阱的意味，因为需要区分是 Arrays.sort() 还是 Collections.sort() （底层是调用 Arrays.sort()）；什么数据类型；多大的数据集（太小的数据集，复杂排序是没必要的，Java 会直接进行二分插入排序）等。

对于原始数据类型，目前使用的是所谓双轴快速排序（Dual-Pivot QuickSort），是一种改进的快速排序算法，早期版本是相对传统的快速排序，你可以阅读源码。
而对于对象数据类型，目前则是使用TimSort，思想上也是一种归并和二分插入排序（binarySort）结合的优化排序算法。TimSort 并不是 Java 的独创，简单说它的思路是查找数据集中已经排好序的分区（这里叫 run），然后合并这些分区来达到排序的目的。

另外，Java 8 引入了并行排序算法（直接使用 parallelSort 方法），这是为了充分利用现代多核处理器的计算能力，底层实现基于 fork-join 框架（专栏后面会对 fork-join 进行相对详细的介绍），当处理的数据集比较小的时候，差距不明显，甚至还表现差一点；但是，当数据集增长到数万或百万以上时，提高就非常大了，具体还是取决于处理器和系统环境。

排序算法仍然在不断改进，最近双轴快速排序实现的作者提交了一个更进一步的改进，历时多年的研究，目前正在审核和验证阶段。根据作者的性能测试对比，相比于基于归并排序的实现，新改进可以提高随机数据排序速度提高 10%～20%，甚至在其他特征的数据集上也有几倍的提高，有兴趣的话你可以参考具体代码和介绍：
http://mail.openjdk.java.net/pipermail/core-libs-dev/2018-January/051000.html 。