1. BF(Brute-Force)

1.1. 算法思想

BF 算法中的 BF 是 Brute Force 的缩写，中文叫作暴力匹配算法，也叫朴素匹配算法。从名字可以看出，这种算法的字符串匹配方式很“暴力”，当然也就会比较简单、好懂，但相应的性能也不高。　

作为最简单、最暴力的字符串匹配算法，BF 算法的思想可以用一句话来概括，那就是，我们在主串中，检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串，看有没有跟模式串匹配的。我举一个例子给你看看，你应该可以理解得更清楚。

1.2. 代码实现

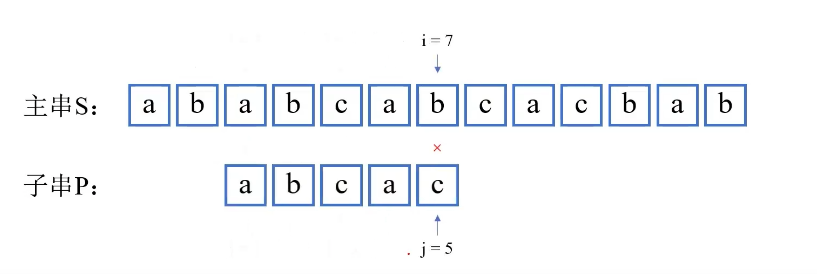
i-j+2可以理解为i-(j-1)+1，(j-1)表示失配前主串移动了几步，主串要回溯这一部分，然后再加1步。比如上图主串从i=3开始，子串从j=1开始，走到了j=5的时候发生了失配，主串要回溯(j-1)即(5-1)步之后，再从后面1步开始比对。而子串回溯到开头。

1.3. 时间复杂度

从上面的算法思想和例子，我们可以看出，在极端情况下，比如主串是“aaaaa…aaaaaa”（省略号表示有很多重复的字符 a），模式串是“aaaaab”。我们每次都比对 m 个字符，要比对 n-m+1 次，所以，这种算法的最坏情况时间复杂度是 O(n*m)。

2. RK算法

2.1. 算法思想

RK 算法的全称叫 Rabin-Karp 算法，是由它的两位发明者 Rabin 和 Karp 的名字来命名的。它其实就是刚刚讲的 BF 算法的升级版。通过哈希算法对主串中的 n-m+1 个子串分别求哈希值，然后逐个与模式串的哈希值比较大小，来降低 BF 算法的时间复杂度。

2.2. 时间复杂度

整个 RK 算法包含两部分，计算 子串哈希值 和 模式串 哈希值与 子串 哈希值之间的比较。
对于 模式串哈希值 与每个 子串哈希值 之间的比较的时间复杂度是 O(1)，通过哈希算法计算子串的哈希值的时候，需要遍历子串中的每个字符。
总共需要比较 n-m+1 个子串的哈希值，所以，这部分的时间复杂度也是 O(n)。所以，RK 算法整体的时间复杂度就是 O(n)。

如果设计的 Hash 算法存在冲突，则在 hash 值相同时比较比一下子串和模式串本身，类似于 hashcode 和 equals 方法

哈希算法的冲突概率要相对控制得低一些，如果存在大量冲突，就会导致 RK 算法的时间复杂度退化，效率下降。极端情况下，如果存在大量的冲突，每次都要再对比子串和模式串本身，那时间复杂度就会退化成 O(n*m)。但也不要太悲观，一般情况下，冲突不会很多，RK 算法的效率还是比 BF 算法高的。

3. BM 算法

3.1. 算法思想

我们把模式串和主串的匹配过程，看作模式串在主串中不停地往后滑动。当遇到不匹配的字符时，BF 算法和 RK 算法的做法是，模式串往后滑动一位，然后从模式串的第一个字符开始重新匹配。
而 BM 算法，全称是 Boyer-Moore 算法，其核心思想是：在模式串中某个字符与主串不能匹配的时候，将模式串往后 多滑动几位，以此来减少不必要的字符比较，提高匹配的效率。

前面两节讲的算法，在匹配的过程中，我们都是按模式串的下标从小到大的顺序，依次与主串中的字符进行匹配的。这种匹配顺序比较符合我们的思维习惯，而 BM 算法的匹配顺序比较特别，它是按照模式串下标从大到小的顺序，倒着匹配的。

3.1.1. 坏字符规则

按模式串 倒序匹配 过程中，把匹配失败时 主串中 的字符，叫作坏字符。然后在模式串中查找坏字符，若找到匹配字符，则将模式串中的 匹配字符 和 坏字符 对齐，否则直接将模式串滑动到 坏字符之后的一位，再重复进行上述过程。

模式串中没有坏字符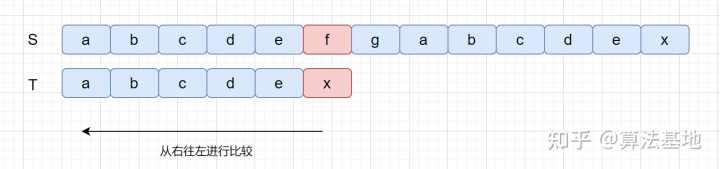

模式串中有1个坏字符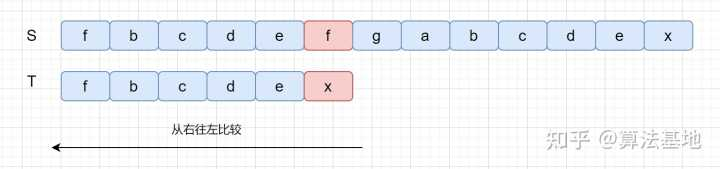

如果 坏字符 在 模式串 里多处出现，选择最靠后的那个，因为这样不会让模式串 滑动过多，导致本来可能匹配的情况被滑动略过。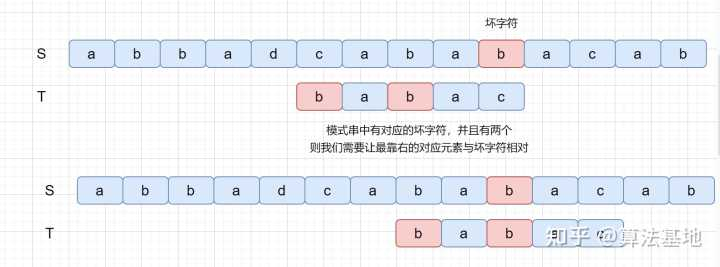

注意：单纯采用坏字符的策略，计算出来的移动位数有可能是负数，因此 BM 算法还需要使用好后缀规则来避免这种情况。因此，在该算法中可以省略坏字符规则，却不能省略好后缀规则。

3.1.1.1. 移动位数

当发生不匹配的时候，我们把坏字符对应的模式串中的字符下标记作 si。如果坏字符在模式串中存在，我们把这个坏字符在模式串中的下标记作 xi。如果不存在，我们把 xi 记作 -1。那模式串往后移动的位数就等于 si-xi。（注意，我这里说的下标，都是字符在模式串的下标）
利用坏字符规则，BM 算法在最好情况下的时间复杂度非常低，是 O(n/m)。比如，主串是 aaabaaabaaabaaab，模式串是 aaaa。每次比对，模式串都可以直接后移四位，所以，匹配具有类似特点的模式串和主串的时候，BM 算法非常高效。

3.1.2. 好后缀规则

这里如果我们按照坏字符进行移动是不合理的，这时我们可以使用好后缀规则，那么什么是好后缀呢？

BM 算法是从右往左进行比较，发现坏字符的时候此时 cac 已经匹配成功，在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀，此时我们拿它在模式串中查找，如果找到了另一个和好后缀相匹配的串，那我们就将另一个和好后缀相匹配的串，滑到和好后缀对齐的位置。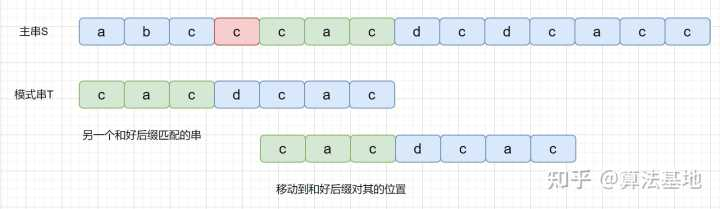

值得注意的是防止过度滑动，滑动时我们不仅要看好后缀在模式串中，是否有另一个匹配的子串，我们还要考察好后缀的后缀子串，是否存在跟模式串的前缀子串匹配的。

4. KMP算法

4.1. Next数组的作用

最长相等前后缀的妙处：我们为了减少复杂度，要尽最大可能减少回溯，也就是尽最大可能让模式串往右移动，想办法跳过那些明显不能匹配成功的位置。往右移动的越多，遍历的次数越少。但是，如果移动多了，会错过匹配。又为了防止错过匹配，那么需要得到最长相等前后缀的信息，来指导模式串回溯到哪个位置。

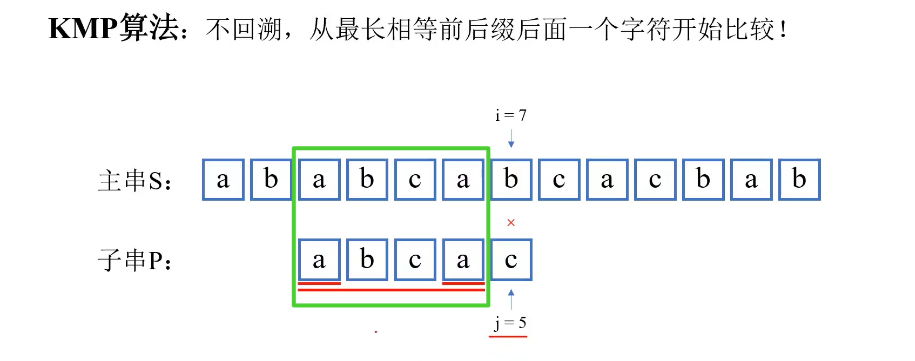
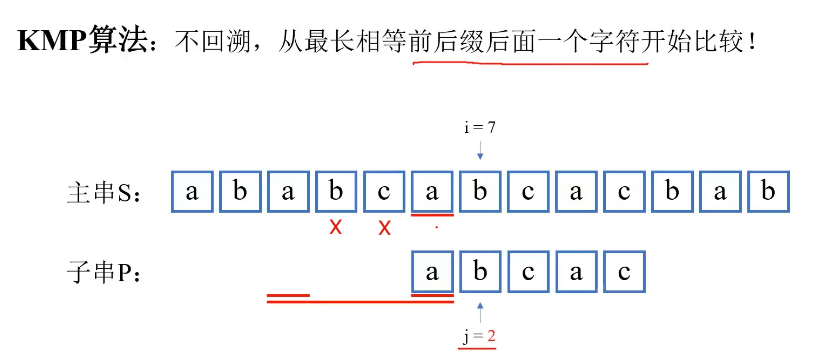
如果是BF，还需要比较b和c这2种不可能的情况

4.2. Next数组的求法

4.2.1. 手动计算

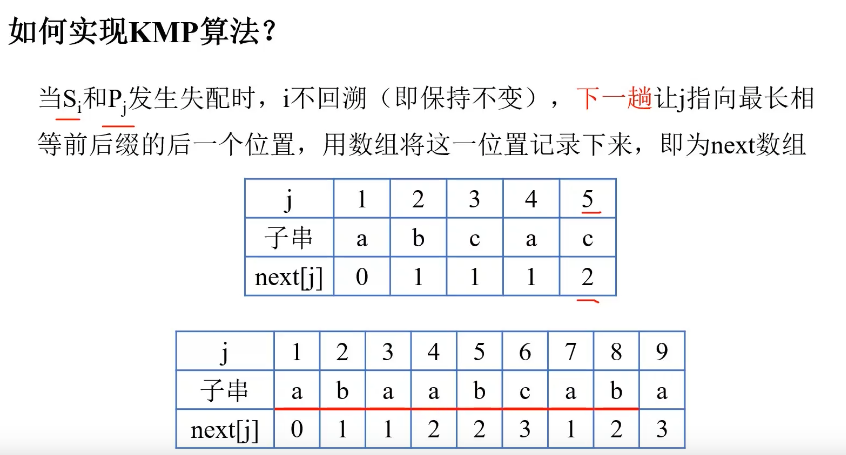
固定前2位分别为0和1，相当于递归的初始化数据部分
j=3时，前2位的最大相等前后缀长度为0，0+1=1
j=4时，前3位的最大相等前后缀长度为1，1+1=2
j=5时，前4位的最大相等前后缀长度为1，1+1=2
j=6时，前5位的最大相等前后缀长度为2，2+1=3
j=7时，前6位的最大相等前后缀长度为0，0+1=1
j=8时，前7位的最大相等前后缀长度为1，1+1=2
j=9时，前8位的最大相等前后缀长度为2，2+1=3

1
2
3

next[5] = 2，有2层含义：
1. P[0~5-1]这一段字符串的最大相等前后缀的长度为2-1
2. 如果在j=5的时候，模式串与主串发生失配时，模式串j回溯后，从j=2开始匹配

4.2.2. 递归计算

4.2.2.1. 理解方式1

因为我们的next[]的定义就是**当与主串发生失配时，模式串回溯的位置，取最大相同前后缀长度的后一位**

例如此处已知 j=5,k=2，接下来要怎么做？

1
2
3

1. 字串再加1位，求next[6]，我们希望新加上的第6位c与第3位相同，那么就可以直接得出 k=k+1 了
2. 所以，就相当于把4、5、6位的“abc”当做主串，把1、2、3位的“aba”当做子串，拿“aba”去“abc”里匹配，这里就是递归的体现之处。abc是第j个字符，aba是第k个字符，请看下图
3. 接下来我们秉承KMP思想的精髓，模式串aba要回溯，当前位置是k，回溯位置是next[k]，所以有 k = next[k]

4.2.2.2. 理解方式2

首先说一句：快速构建next数组，是KMP算法的精髓所在，核心思想是“P自己与自己做匹配”。

为什么这样说呢？因为失配前，主串和模式串是重合的，也就是相等的
　　
回顾next数组的完整定义：

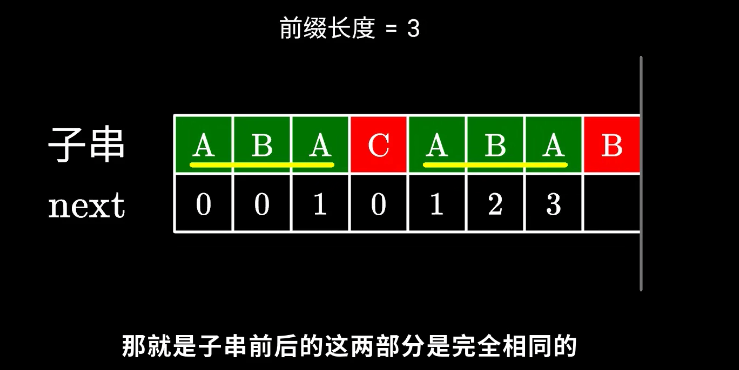
定义 “k-前缀” 为一个字符串的前 k 个字符； “k-后缀” 为一个字符串的后 k 个字符。k 必须小于字符串长度。
next[x] 定义为： P[0]~P[x] 这一段字符串，使得k-前缀恰等于k-后缀的最大的k.

　　这个定义中，不知不觉地就包含了一个匹配——前缀和后缀相等。接下来，我们考虑采用递推的方式求出next数组。如果next[0], next[1], … next[x-1]均已知，那么如何求出 next[x] 呢？

　　我们来分情况讨论。首先，已经知道了 next[x-1]（以下记为now），如果 P[x] 与 P[now] 一样，那最长相等前后缀的长度就可以扩展一位，很明显 next[x] = now + 1. 图示如下。
　　

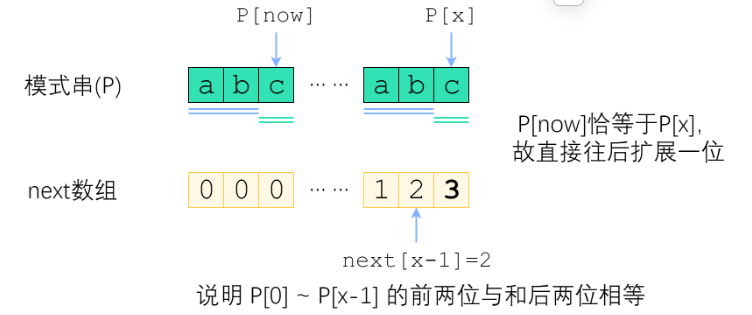
刚刚解决了 P[x] = P[now] 的情况。那如果 P[x] 与 P[now] 不一样，又该怎么办？

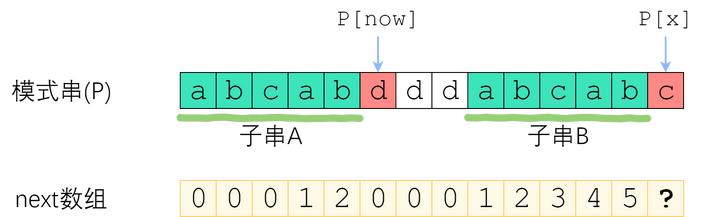
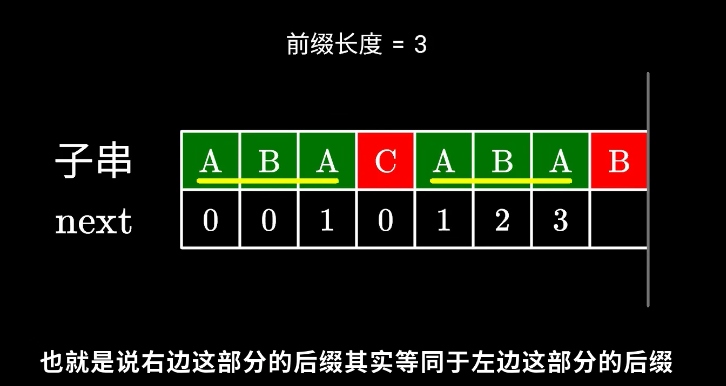
如图。长度为 now 的子串 A 和子串 B 是 P[0]~P[x-1] 中最长的公共前后缀。可惜子串 A 右边的字符和子串B 右边的那个字符不相等，next[x]不能直接变为 now+1 了。因此，我们应该缩短这个now，把它改成小一点的值，再来试试 P[x] 是否等于 P[now].

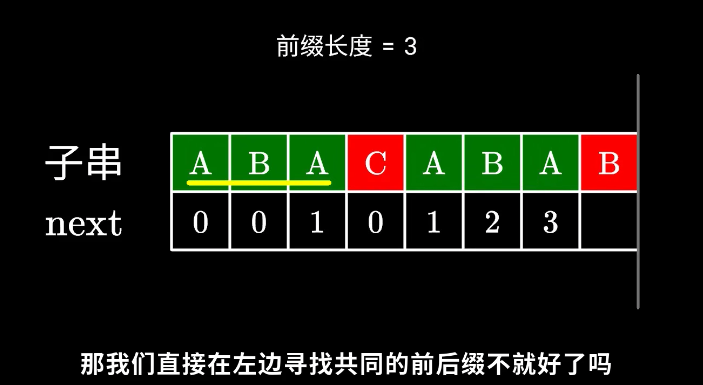
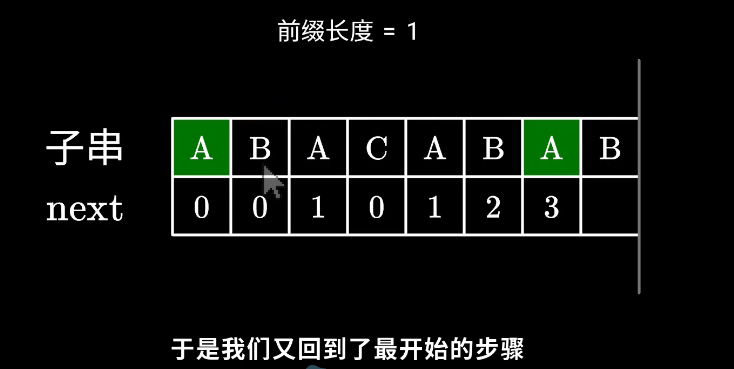
步骤为：先求P[0x-1]这串字符串的最大相同前后缀长度，也就是next[now-1]。然后回溯到next[now-1]的位置，即 now = next[now-1]，再判断此时的P[now]是否等于P[x]，如果相等，则now=now+1，否则继续回溯，重复上述过程。
　　
为什么缩短now，now该缩小到多少呢？
显然，我们不想让now缩小太多。因此我们决定，在保持“P[0]P[x-1]的[now-前缀]仍然等于[now-后缀]”的前提下，让这个新的now尽可能大一点。又因为P[0]~P[x-1] 的公共[前后缀]，前缀一定落在子串A里面、后缀一定落在子串B里面。换句话讲：接下来now应该改成：使得 A的[k-前缀]等于B的[k-后缀] 的最大的k.
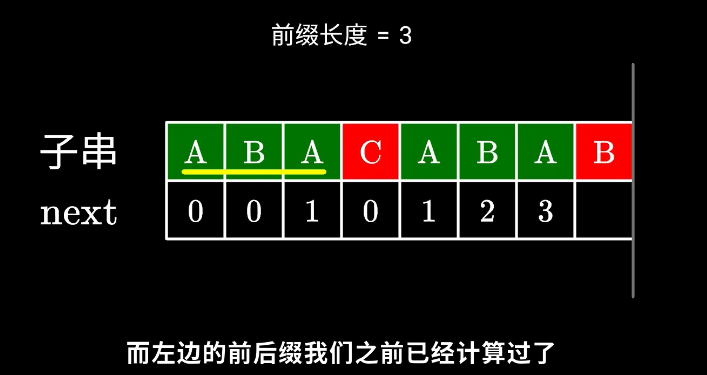
此时我们应该已经注意到了一个非常强的性质——子串A和子串B是相同的！那么B的后缀也就等于A的后缀！因此，使得A的k-前缀等于B的k-后缀的最大的k，其实就是求子串A的最长相同前后缀的长度 —— next[now-1]！也就是 now = next[now-1]

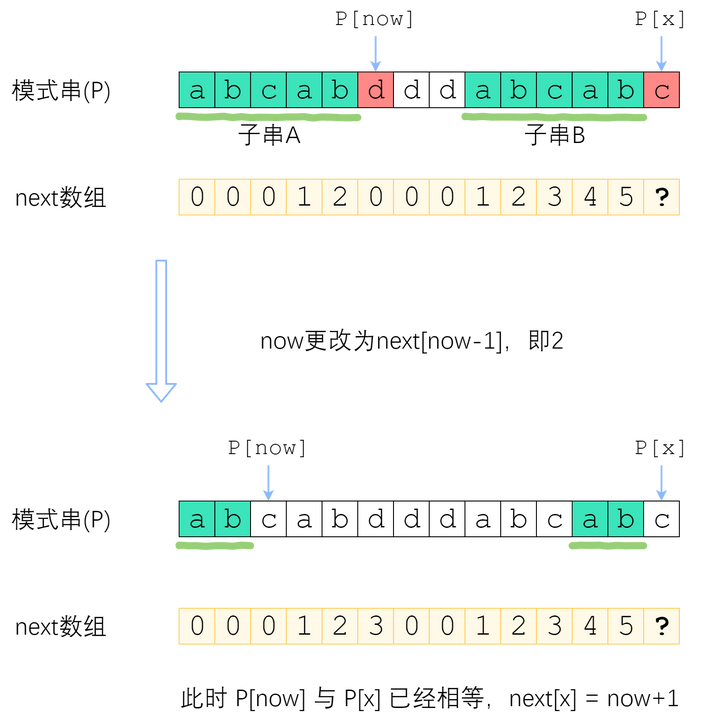
来看上面的例子。当P[now]与P[x]不相等的时候，我们需要缩小now——把now变成next[now-1]，直到P[now]=P[x]为止。P[now]=P[x]时，就可以直接向右扩展了。

4.2.2.3. 理解方式3

实质同理解2

4.3. KMP问题

第一部分是构建 next 数组

第二部分借助 next 数组匹配

4.4. 时间复杂度

KMP 算法包含两部分，第一部分是构建 next 数组，第二部分才是借助 next 数组匹配。所以，关于时间复杂度，我们要分别从这两部分来分析。

构建 next 数组，j 从 1 开始一直增加到 m，而 k 并不是每次 for 循环都会增加，所以，k 累积增加的值肯定小于 m。而 while 循环里 k=next[k]，实际上是在减小 k 的值，k 累积都没有增加超过 m，所以 while 循环里面 k=next[k] 总的执行次数也不可能超过 m。因此，next 数组计算的时间复杂度是 O(m)。

我们再来分析第二部分的时间复杂度。分析的方法是类似的。

i 从 0 循环增长到 n-1，j 的增长量不可能超过 i，所以肯定小于 n。而 while 循环中的那条语句 j=next[j]+1，不会让 j 增长的，那有没有可能让 j 不变呢？也没有可能。因为 next[j] 的值肯定小于 j，所以 while 循环中的这条语句实际上也是在让 j 的值减少。而 j 总共增长的量都不会超过 n，那减少的量也不可能超过 n，所以 while 循环中的这条语句总的执行次数也不会超过 n，所以这部分的时间复杂度是 O(n)。

所以，综合两部分的时间复杂度，KMP 算法的时间复杂度就是 O(m+n)。